MEDIDAS DE DISPERSIÓN

 

Varianza y desviación estándar

Veamos la varianza y la desviación estándar de la muestra y de la población, con ejercicios, ejemplos y veamos también las fórmulas.

 La varianza y la desviación estándar son medidas de dispersión o variabilidad, es decir, indican la dispersión o separación de un conjunto de datos. Hay que tener en cuenta que las fórmulas de la varianza y la desviación estándar son diferentes para una muestra que para una población.

 A continuación, presentamos el resumen de fórmulas, las cuales analizaremos líneas abajo: 

 

Varianza de la población (σ²)

La varianza se define como la media aritmética de los cuadrados de las diferencias de los datos con su media aritmética. 

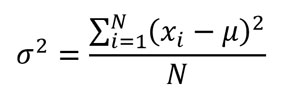
Desviación estándar de la población (σ)

La desviación estándar es la raíz cuadrada positiva de la varianza.

Te recomendamos calcular primero la varianza de la población y luego sacar su raíz cuadrada para obtener la desviación estándar.

Ten en cuenta que, si tienes una serie de valores de una población y necesitas calcular su varianza y su desviación estándar, deberás calcular primero la media poblacional µ con la siguiente fórmula:

Varianza de la muestra (s²)

La fórmula de la varianza de la muestra es diferente a la de varianza de la población.

Desviación estándar de la muestra (s)

Recuerda que la desviación estándar es la raíz cuadrada positiva de la varianza.

Te recomendamos calcular primero la varianza de la muestra y luego sacar su raíz cuadrada para obtener la desviación estándar.

Ten en cuenta que, si tienes una serie de valores de una muestra y necesitas calcular su varianza y su desviación estándar, deberás calcular primero la media poblacional x̄ con la siguiente fórmula:

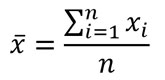
Medidas de asimetría, curtosis y sesgo Son aquellos números resúmenes, que indican la morfología de la distribución de los datos, es decir de la simetría y apuntamiento que tiene el histograma de la variable en estudio. Sólo se pueden calcular en variables medidas en escala intervalo y de razón. Son el:  sesgo (coeficiente de asimetría)  Cucurtosis  COEFICIENTE DE ASIMETRÍA  Mide el grado de asimetría de la distribución con respecto a la media. Un valor positivo de este indicador significa que la distribución se encuentra sesgada hacia la izquierda (orientación positiva). Un resultado negativo significa que la distribución se sesga a la derecha. CURTOSIS  Indica que tan apuntada o achatada se encuentra una distribución respecto a un comportamiento normal (distribución normal).  Si los datos están muy concentrado hacia la media, la distribución es leptocúrtica (curtosis mayor a 0). Si los datos están muy dispersos, la distribución es platicúrtica (curtosis menor a 0). El comportamiento normal exige que la curtosis sea igual a 0 (distribución mesocúrtica). COMO ACTIVIDAD PARA REFORZAR ESTOS TEMAS REALIZAMOS LOS SIGUIENTES EJERCICIOS QUE SE ENCUENTRAN EN LOS SIGUIENTES LINKS: https://es.khanacademy.org/math/cc-sixth-grade-math/cc-6th-data-statistics/cc-6-mad/e/calculating-the-mean-absolute-deviation--mad- https://es.khanacademy.org/math/statistics-probability/summarizing-quantitative-data/variance-standard-deviation-population/a/calculating-standard-deviation-step-by-step